This is another post of the series where I explain some ideas I tried in order to improve the upscaling of the half-resolution SSAO render target of the VKDF sponza demo that was written by Iago Toral. In the previous post, I had classified the sample neighborhoods in surface neighborhoods and neighborhoods that contain depth discontinuities using the normals. Having this information about the neighborhoods, in this post, I will try to further improve the nearest depth algorithm (see also parts 1 and 2) and reduce the artifacts in the neighborhoods where we detect depth discontinuities.
Before I start a quick overview of my previous posts:
- In part 1 we’ve seen that the nearest depth algorithm by NVIDIA can reduce the artifacts where we have depth discontinuities but cannot improve significantly the overall upsampling quality.
- In part 2 we’ve seen that downsampling the z-buffer by taking the maximum sample of each 2×2 neighborhood or by taking once the minimum and once the maximum following a checkerboard pattern works well with the nearest depth but the overall quality is still very bad.
- In part 3.1 we’ve seen that it is possible to use different upscaling algorithms for the surfaces and the regions where we detect depth discontinuities. The idea was to use some sort of weighted average when all the samples of a neighborhood belong to the same surface and the nearest depth algorithm when we detect a depth discontinuity (not all samples belong to the same surface). We tried to classify the sample neighborhoods to “surface neighborhoods” and “discontinuity neighborhoods” using only depth information and we’ve seen that this is not working well as the method depends on what is visible on the screen and on the near and far clipping planes positions.
- In part 3.2 we’ve seen that downscaling the normal buffer using the same algorithm we used to downscale the z-buffer and using the normals to understand if a neighborhood belongs to a surface or contains a depth discontinuity works very well, but performing lerp on surfaces and nearest depth on discontinuities still causes some visible artifacts that we could maybe reduce with other algorithms.
Also, improving the SSAO texture upsampling with a “depth-aware” method involves 2 parts:
- Improving the z-buffer downsampling to preserve the representation of the surfaces from the original z-buffer.
- Improving the SSAO texture upsampling using information from the low resolution z-buffer.
and the upsampling can be improved in 2 different ways depending on the type of each 2×2 neighborhood:
- By achieving smoother colors on the surfaces.
- By selecting better depths where we have discontinuities to improve the nearest depth.
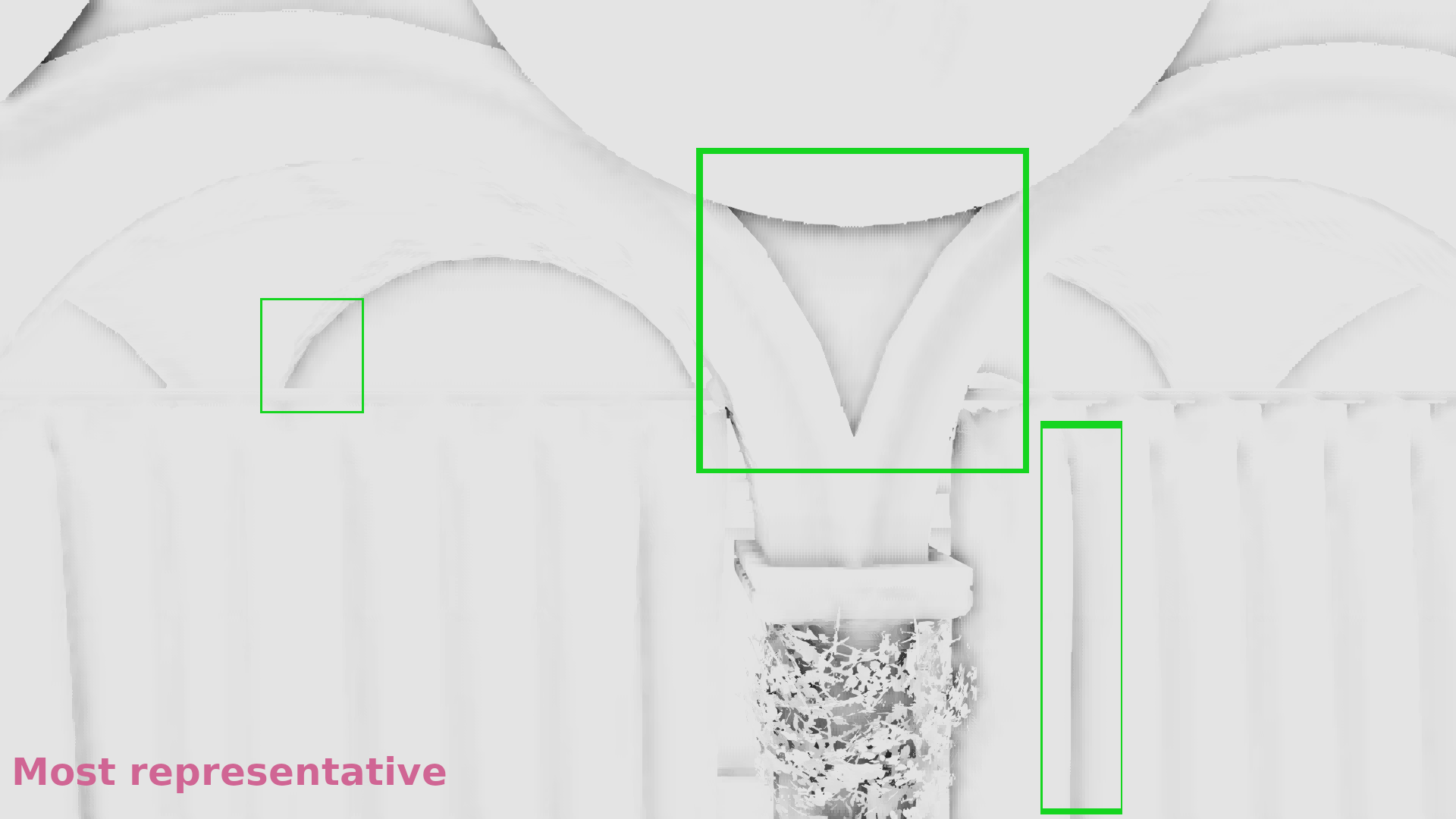
In this post, we will focus on improving the upsampling in the regions that contain discontinuities. Thanks to the classification using the normal (see part 3.2) we can detect these regions quite accurately. In the image below they are the ones in black color:

In these regions, we still use the nearest depth algorithm from NVIDIA that we’ve analyzed in parts 1 and 2. As we’ve seen, improving the quality of the nearest depth can be achieved by improving the original depth buffer downsampling that takes place in a separate pass and whose output is used as input where the SSAO render target is upscaled (usually lighting pass).
So, in this post, we will discuss further z-buffer downscaling improvements but this time paying more attention to the regions where we have discontinuities.
Some thoughts:
Should we classify the pixels during the downsampling?
One thing I was wondering about, was if it would be worth classifying the samples during the z-buffer downsampling part. Could I achieve a better AO quality by preserving different depth information on the surfaces and different where I detect discontinuities? At first, I thought this could be a good idea to try but soon I realized that a classification during the downsampling would only add extra complexity and for no obvious reason:
As the depth samples that lie on the same surface will have similar depth values, it doesn’t matter so much if we select the minimum, the maximum or the mediump among them, any sample is quite representative of its neighborhood depths as all the depths have values really close to each other.
So, at the end, I just forgot about the surfaces and tried to improve the downsampling to preserve the information where we have discontinuities. (Besides, as the weighted average on the surfaces had a clear advantage over the best depth as we have seen in Part 3.2, I was almost sure that at the end I wouldn’t use any depths for the upsampling on the surfaces anyway).
So, my next question was:
Could we somehow select a better depth?
So far (in part 2) we’ve seen that the maximum depth and the selection of the minimum and the maximum depth sequentially following a checkerboard pattern works well in discontinuities but there was no big difference between the two. So my next idea here, was to not use the maximum or the minimum at all, but try to find the most representative depth of the neighborhood.
Let’s see how:
Selecting the most representative depth sample of each 2×2 neighborhood
In each 2×2 neighborhood we find the centroid (in our case the centroid equals the average depth). Then we calculate each depth’s distance from this centroid and we reject the sample that has the maximum one. Then, we calculate a new centroid and new distances for the remaining 3 depth samples and we reject again the sample with the maximum distance. We repeat for the last two samples. (If the samples were colors we could average the remaining two and return the result but here we don’t want to create depths that don’t exist in the original depth buffer so averaging the last two samples is a bad idea!)
The algorithm is quite more complex than the ones we’ve seen in Part 2 and I was expecting that it would be too slow and I would probably need to find some way to approximate it. To my surprise it wasn’t (I’ll talk about performance later in this post). So here’s a straight forward GLSL implementation (I am pretty sure that there are better ways to write the following code!:p)
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 |
float most_representative(sampler2D tex_depth, vec2 in_uv) { float d[] = float[] ( textureOffset(tex_depth, in_uv, ivec2(0, 0)).x, textureOffset(tex_depth, in_uv, ivec2(0, 1)).x, textureOffset(tex_depth, in_uv, ivec2(1, 0)).x, textureOffset(tex_depth, in_uv, ivec2(1, 1)).x); float centr = (d[0] + d[1] + d[2] + d[3]) / 4.0; float dist[] = float[] ( abs(centr - d[0]), abs(centr - d[1]), abs(centr - d[2]), abs(centr - d[3])); float max_dist = max(max(dist[0], dist[1]), max(dist[2], dist[3])); float d3[3]; int j = 0; for (int i = 0; i < 4; i++) { if (dist[i] <= max_dist && j < 3) { d3[j] = d[i]; j++; } } centr = (d3[0] + d3[1] + d3[2]) / 3.0; dist[0] = abs(d3[0] - centr); dist[1] = abs(d3[1] - centr); dist[2] = abs(d3[2] - centr); float d2[2]; j = 0; max_dist = max(max(dist[0], dist[1]), dist[2]); for (int i = 0; i < 3; i++) { if (dist[i] <= max_dist && j < 2) { d2[j] = d3[i]; j++; } } centr = (d2[0] + d2[1]) / 2.0; dist[0] = abs(d2[0] - centr); dist[1] = abs(d2[1] - centr); if (dist[0] < dist[1]) return d2[0]; return d2[1]; } |
The downsampling is then simple (I pack the normals and the depths in the same color attachment here):
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
float d[] = float[] ( textureOffset(tex_depth, in_uv, ivec2(0, 0)).x, textureOffset(tex_depth, in_uv, ivec2(0, 1)).x, textureOffset(tex_depth, in_uv, ivec2(1, 0)).x, textureOffset(tex_depth, in_uv, ivec2(1, 1)).x); vec3 n[] = vec3[] ( textureOffset(tex_normal, in_uv, ivec2(0, 0)).xyz, textureOffset(tex_normal, in_uv, ivec2(0, 1)).xyz, textureOffset(tex_normal, in_uv, ivec2(1, 0)).xyz, textureOffset(tex_normal, in_uv, ivec2(1, 1)).xyz); /* float best_depth = max(max(d[0], d[1]), max(d[2], d[3])); float best_depth = mix(max(max(d[0], d[1]), max(d[2], d[3])), min(min(d[0], d[1]), min(d[2], d[3])), checkerboard(in_uv)); */ float best_depth = most_representative(tex_depth, in_uv); for (int i = 0; i < 4; i++) { if (best_depth == d[i]) { out_color = vec4(n[i], d[i]); return; } } |
If we need to combine it with lerp on the surfaces, then in the SSAO upsampling pixel shader we can do the classification using the normal that we’ve already analyzed in Part 3.2:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
vec3 n[] = vec3[] ( textureOffset(tex_ssao_dnbuf, in_uv, ivec2(0, 0)).rgb, textureOffset(tex_ssao_dnbuf, in_uv, ivec2(0, 1)).rgb, textureOffset(tex_ssao_dnbuf, in_uv, ivec2(1, 0)).rgb, textureOffset(tex_ssao_dnbuf, in_uv, ivec2(1, 1)).rgb); float dot01 = dot(n[0], n[1]); float dot02 = dot(n[0], n[2]); float dot03 = dot(n[0], n[3]); float min_dot = min(dot01, min(dot02, dot03)); float s = step(0.992, min_dot); return mix(nearest_depth_ao(tex_ssao_nearest, tex_ssao_dnbuf, tex_depth, in_uv), lerp_ao(tex_ssao, in_uv), s); |
where the nearest depth is what we’ve seen in Part 1:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
float d[] = float [] ( textureOffset(tex_ssao_dnbuf, in_uv, ivec2(0, 0)).a, textureOffset(tex_ssao_dnbuf, in_uv, ivec2(0, 1)).a, textureOffset(tex_ssao_dnbuf, in_uv, ivec2(1, 0)).a, textureOffset(tex_ssao_dnbuf, in_uv, ivec2(1, 1)).a); float ao[] = float[] ( textureOffset(tex_ssao_nearest, in_uv, ivec2(0, 0)).r, textureOffset(tex_ssao_nearest, in_uv, ivec2(0, 1)).r, textureOffset(tex_ssao_nearest, in_uv, ivec2(1, 0)).r, textureOffset(tex_ssao_nearest, in_uv, ivec2(1, 1)).r); float d0 = texture(tex_depth, in_uv).r; float min_dist = 1.0; int best_depth_idx; for (int i = 0; i < 4; i++) { float dist = abs(d0 - d[i]); if (min_dist > dist) { min_dist = dist; best_depth_idx = i; } } return ao[best_depth_idx]; |
and the lerp_ao is just the result of the built-in GLSL texture function when the filter of the sampler that was used with the SSAO low resolution texture was VK_FILTER_LINEAR.
Comparing the results
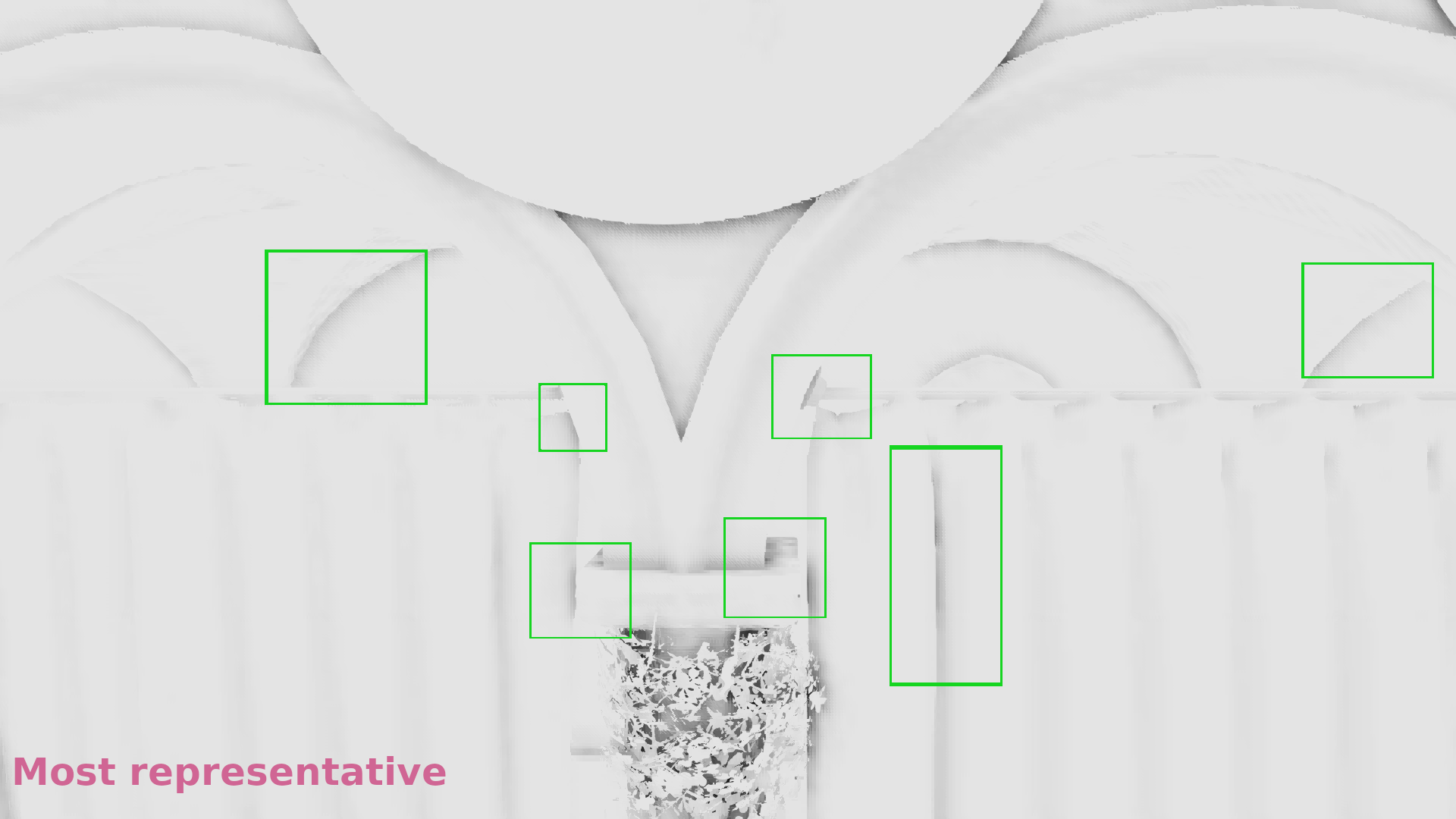
Let’s see some comparisons. Remember that we try to fix the artifacts where we have depth discontinuities (black regions in the image that shows the “discontinuity detection”)
Nearest depth comparison
The galleries below show a comparison of the nearest depth SSAO in 1/4 resolution in the following three cases:
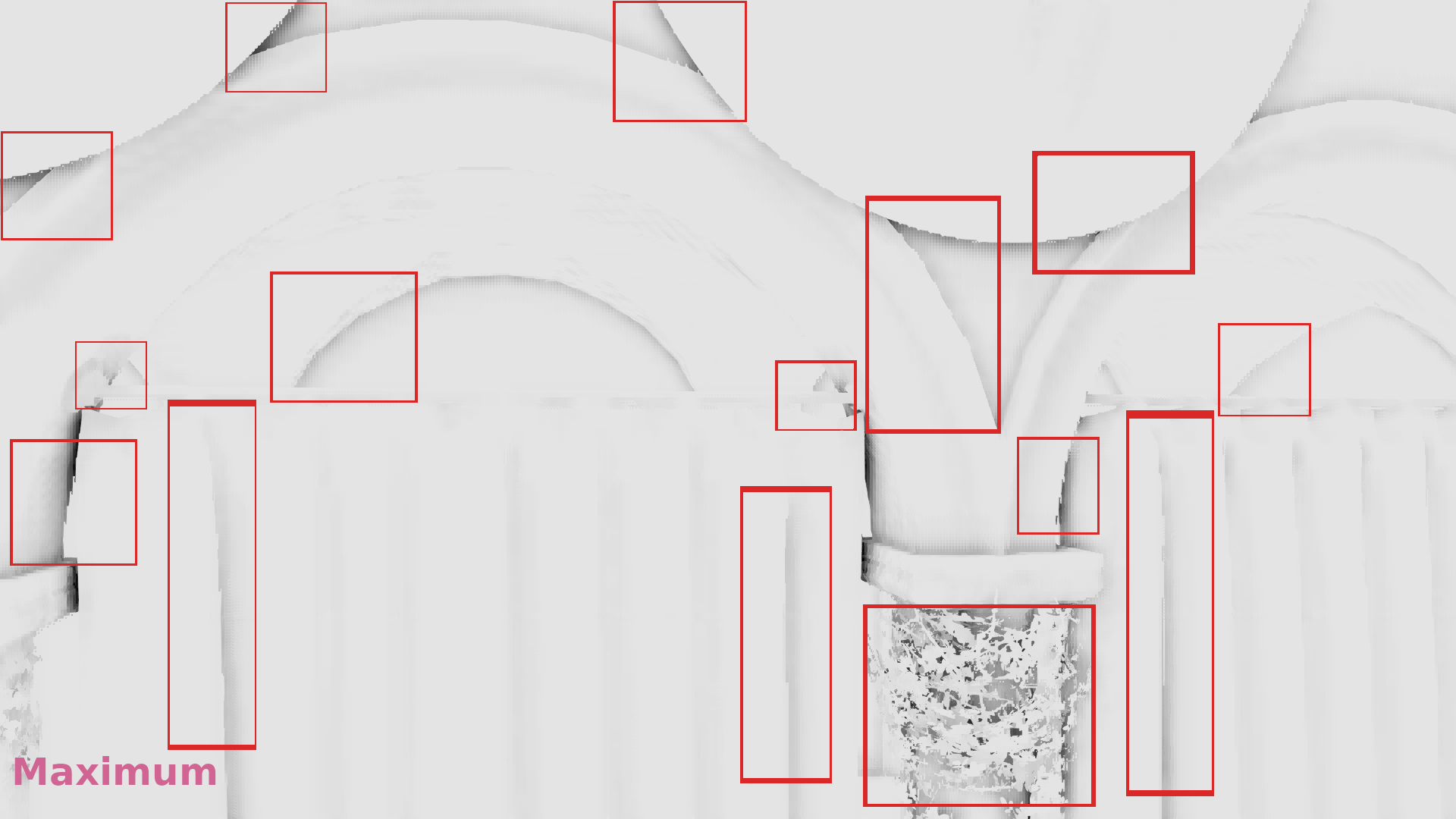
- The z-buffer was downscaled by selecting the maximum depth of each 2×2 neighborhood (article from NVIDIA).
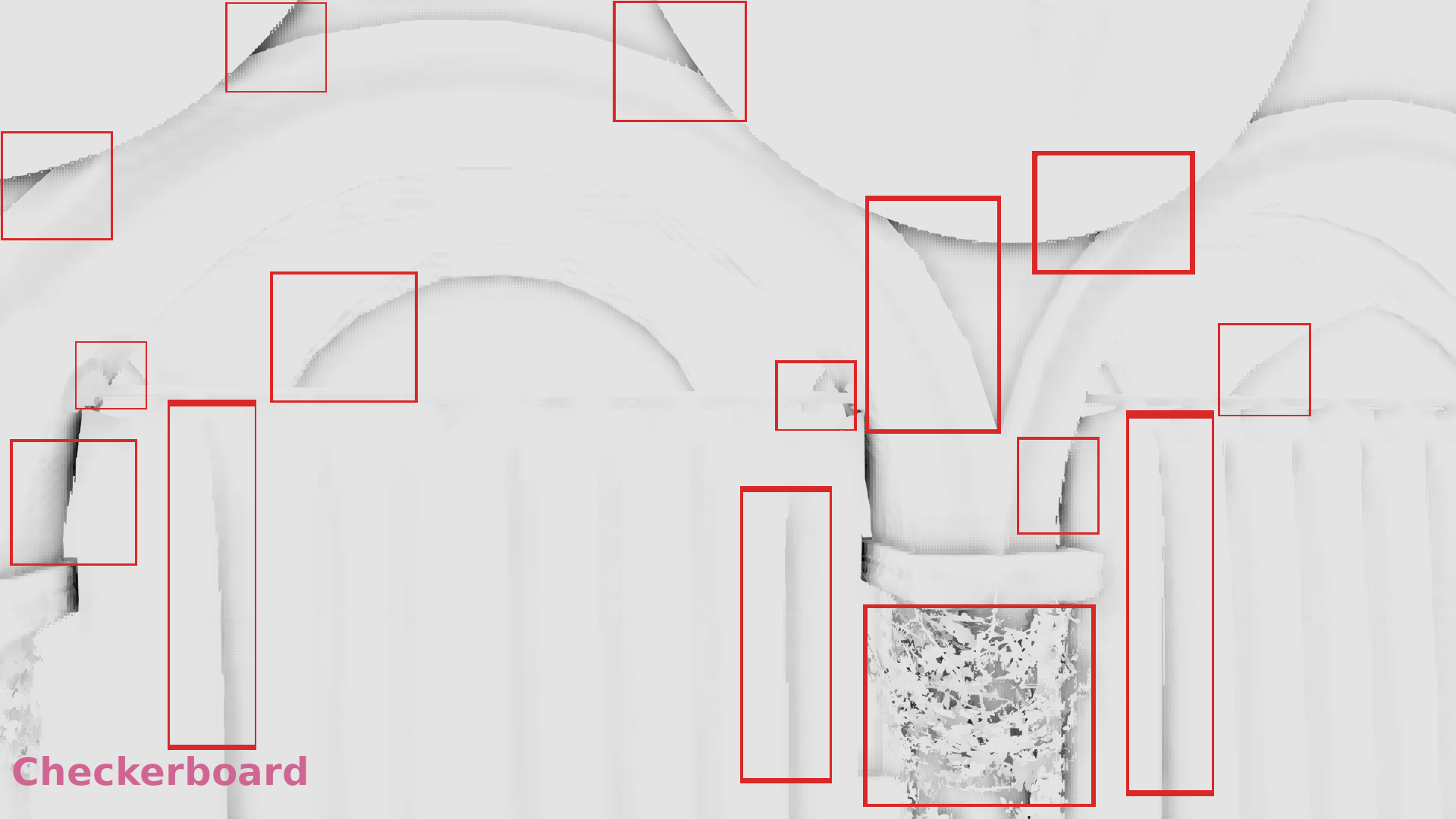
- The z-buffer was downscaled by selecting once the maximum once the minimum depth following a checkerboard pattern (article from Call of Duty Black Ops 3).
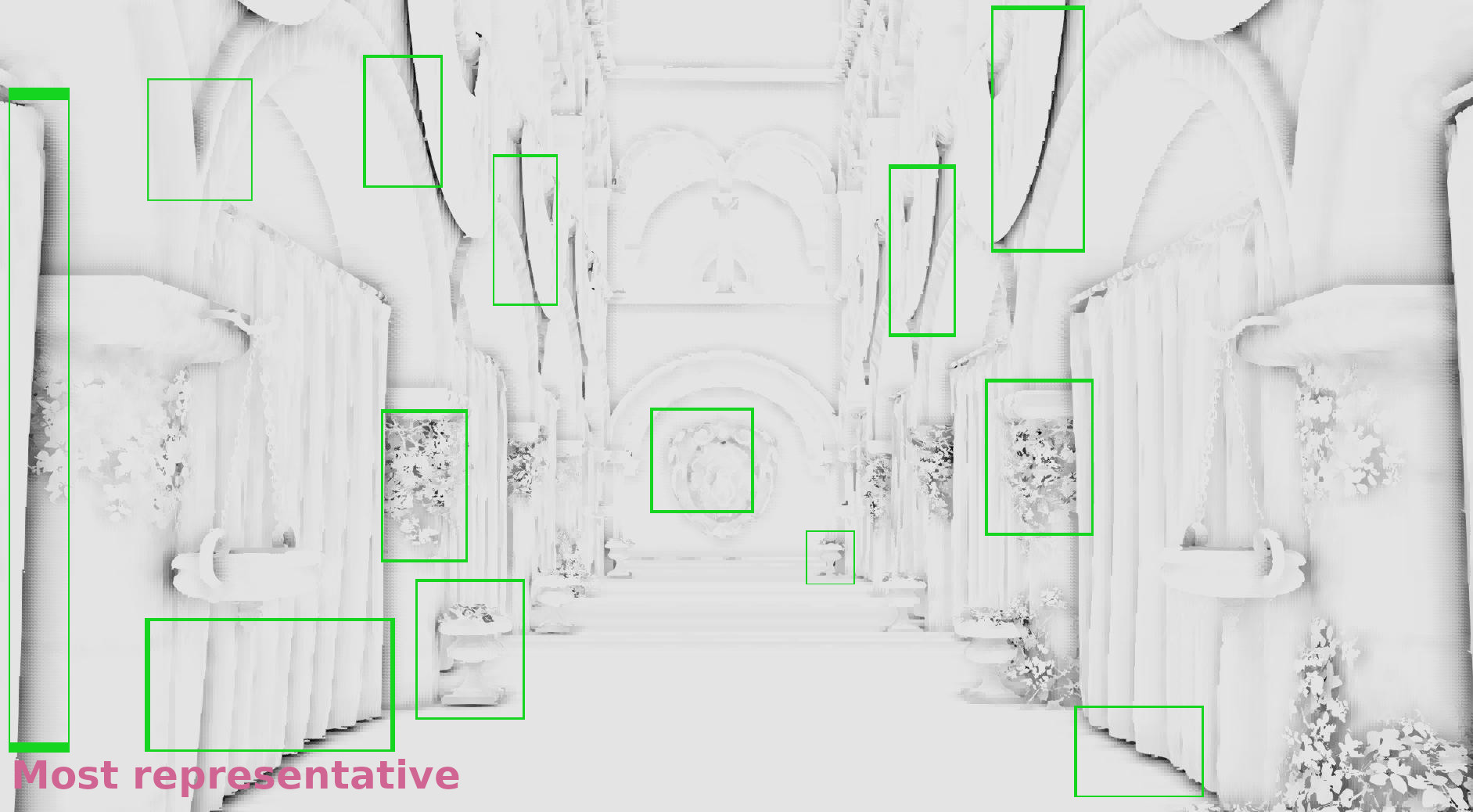
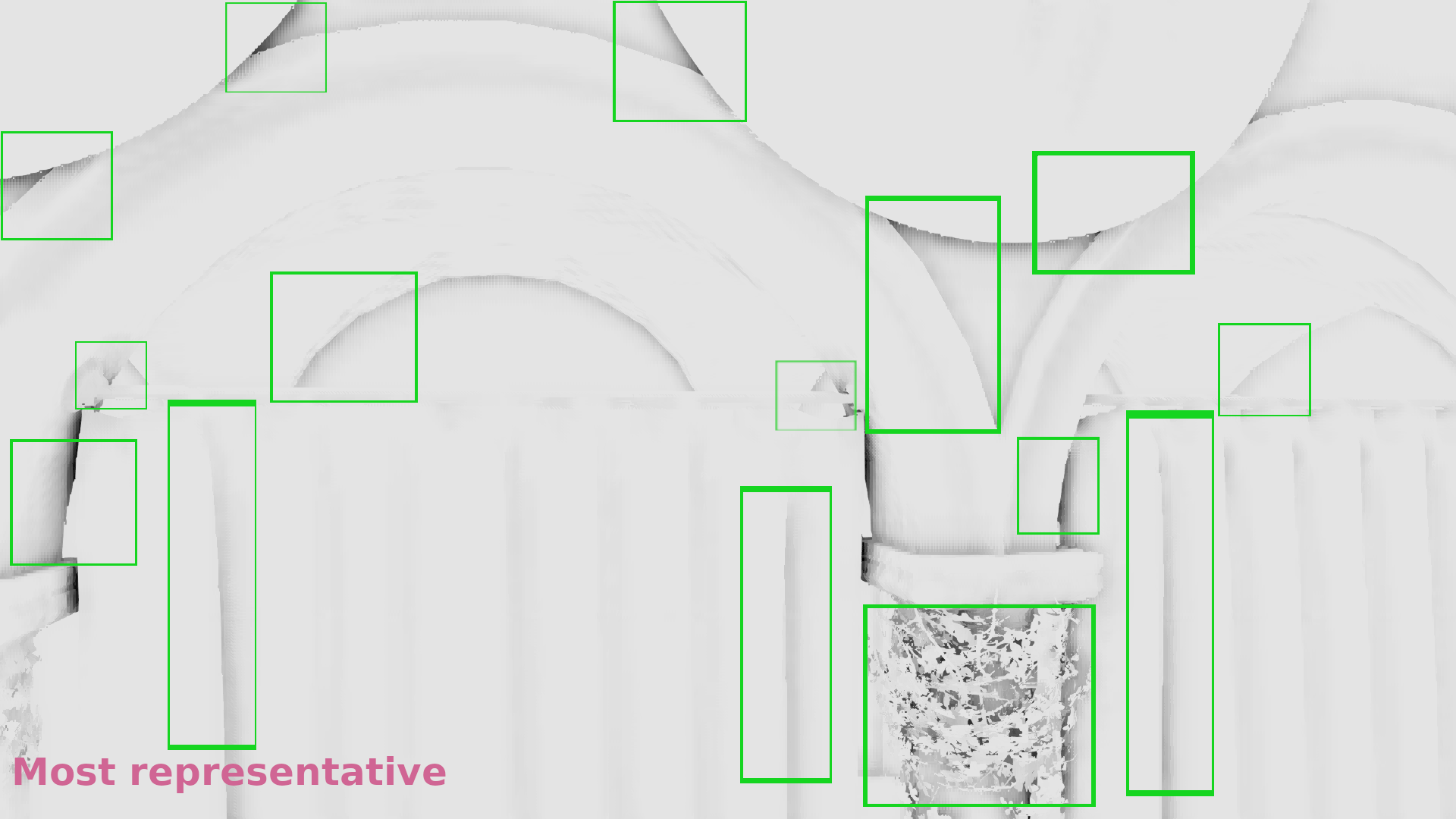
- The z-buffer was downscaled by selecting the most representative depth with the algorithm I’ve just described.
Note: in all posts, I compare the images in 1/4 resolution for the artifacts to be more visible and then I record videos in 1/2 resolution that is the target resolution.
In the galleries below I chose random frames for comparison. In some cases the differences are significant, in some others subtle, but it seems that in general selecting the most representative depth causes less artifacts. (Also I show the discontinuities in 1/2 resolution because the 1/4 above was annoyingly low res to allow observing the image :p).
Frame #323:
Frame #338:
Frame #429:
Frame #475:
Frame #518:
Frame #562:
In 1/2 resolution the advantage of taking the most representative sample during the z buffer downsampling is still visible as you can see in the following video:
and a video of the final result of the nearest depth/most representative:
Linear interpolation on surfaces/Nearest depth on discontinuities
After having seen that selecting the most representative sample during the z-buffer downsampling preserves more the SSAO quality compared to selecting the maximum depth or once the minimum once the maximum following a checkerboard pattern when used with nearest depth, I wanted to check how much different is the result when linear interpolation is used on the surfaces.
I think that the effect of the linear interpolation can become quite obvious in the following frames (1/4 resolution):
Many artifacts (for example shadows in green quads) disappear after smoothing with lerp. But it seems that some regions don’t look so nice (see the yellow quads). Ideally, we would like to further control how we apply the smoothing so that we don’t see many imperfections in surface neighborhoods that are very close to neighborhoods that contain discontinuities (follow-up experiments).
Fortunately, these imperfections aren’t too visible in 1/2 resolution, but they are still present:
Some videos
Comparison between the most representative/nearest depth and the most representative/nearest on discontinuities combined with linear interpolation on surfaces:
I think that the combination of best depth and lerp gives the best results so far (although I tried to further improve the SSAO upsampling on surfaces, future post):
and that this method gives acceptable results (although I plan to post about further improvements):
(the video above is from the “final” rendering so it has all the visual effects enabled like SSR and the others mentioned in Iago’s post)
Performance
In order to reduce the fetches from the video memory and fit more data in the cache I packed the normals and the depths in one color attachment. I used the rgb values to store the xyz of the normal direction and the a to store the depth for each sample (the renderpass parameters are the same I used in Part 3.2).

Then I calculated the SSAO in 1/2 resolution render targets using Iago‘s code and upsampled with different algorithms. Here’s how much each one increased the FPS of the original (full resolution) SSAO:
- Max depth/Nearest depth + Lerp: increased the FPS by
45.7% - Checkerboard/Nearest depth + Lerp: increased the FPS by
45.6% - Most representative/Nearest depth + Lerp: increased the FPS by
45.1%
It seems that the difference in FPS when the most representative sample is selected is not significant. Actually it’s almost unnoticeable! 🙂
Conclusions
Selecting the most representative sample of each 2×2 neighborhood by calculating the distance of the centroid of each subneighborhood and rejecting the sample with the maximum one at each repetition improves the nearest depth algorithm and has no significant difference in performance when compared to other z-buffer downsampling techniques.
The combination of nearest depth using the most representative on discontinuities with linear interpolation on surfaces is a further improvement but it’s not perfect as some regions have new imperfections (not really artifacts but they don’t look so nice) which means that there might still be room for improvement!
Next post
In the next post, we’ll try to find a better method to control the amount of smoothing in each 2×2 neighborhood and we’ll check if there is a way to further reduce the imperfections caused by lerp in surface neighborhoods that are very close to discontinuity neighborhoods.
Videos
As usually, I embedded a playlist of the videos I used for the comparisons, for those who want to examine them one by one.
Links:
Iago‘s post on his VKDF sponza demo: https://blogs.igalia.com/itoral/2018/04/17/frame-analysis-of-a-rendering-of-the-sponza-model/
Other posts of these series:
– part 1: https://eleni.mutantstargoat.com/hikiko/on-depth-aware-upsampling
– part 2: https://eleni.mutantstargoat.com/hikiko/depth-aware-upsampling-2
– part 3.1: https://eleni.mutantstargoat.com/hikiko/depth-aware-upsampling-3-1
– part 3.2: https://eleni.mutantstargoat.com/hikiko/depth-aware-upsampling-3-2
Articles:
On nearest depth (NVIDIA): http://developer.download.nvidia.com/assets/gamedev/files/sdk/11/OpacityMappingSDKWhitePaper.pdf
On upsampling (Call of Duty Black Ops 3): http://c0de517e.blogspot.com/2016/02/downsampled-effects-with-depth-aware.html